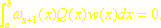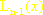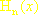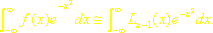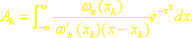6.3 Zastosowanie wielomianów ortogonalnych do całkowania numerycznego.

Dla obliczania numerycznego całek był wzór interpolacyjny Lagrange’a oparty na węzłach rozmieszczonych w jednakowych odstępach. Może zdarzyć się tak, że dla innego rozmieszczenia węzłów dokładność wzorów dla całkowania numerycznego będzie większa.

Twierdzenie 6.4. Kwadratura (6.12) jest dokładna dla wszystkich wielomianów stopnia  ≤  2n+1 wtedy i tylko wtedy, gdy jest ona interpolacyjna oraz wielomian

                                                                        jest ortogonalny względem wszystkich wielomianów Q(x) stopnia mniejszego, niż n+1:

                                                                                                                                                                                                                (6.34)

Twierdzenie 6.5. Węzłami kwadratury dokładnej dla wszystkich wielomianów stopnia  ≤ 2n+1 są pierwiastki odpowiednich wielomianów ortogonalnych.

6.3.2 Wielomiany Hermite’a

Dla obliczania całek postaci

funkcję podcałkową zastępujemy przez wielomian interpolacyjny Lagrange’a ,                 oparty na zerach odpowiedniego wielomianu Hermite’a 

Wtedy otrzymamy

                                                                                                    (6.38)

gdzie

Węzeł i współczynniki dla wzoru (6.38) podane są w tablicy 6.5.

Tablica 6.5

Węzły x_k (zera wielomianów Hermite’a H_n (x)) i współczynników A_k dla wzoru (6.38)